|
| Aktualizováno19.12.2014 |
Základní elektrotechnická zapojení v praxi |
|
Cílem
tohoto projektu je
vytvořit
skripta pro výuku odborného výcviku v
oboru
elektronika a
automatizace. Skripta budou zaměřeny
především na
pratická provádění
měření a jednoduché výpočty v
základních elektronických obvodech
v
návaznosti na teoretické znalosti v oboru
elektronika a
automatizace.Ukázka jednoduchých
zadání pro
práci žáků středních škol,
zabývajících se touto problematikou
|
Měření na derivačním člákuSpočítejte a měřením ověřte derivační článek. Na vstup derivačního článku připojte obdélníkový průběh napětí se střídou 1/1, Umax 2V a kmitočtu 1kHz. Derivační článek spočítejte pro dvě varianty , a to je-li Tau desetkrát větší než doba periody a po druhé tak, aby Tau bylo desetkrát menší než doba periody. Průběhy výstupního napětí měřte osciloskopem a naměřené průběhy na obrazovce osciloskopu zakreslete do sešitu. |
Schéma zapojení |
Teoretické průběhy napětí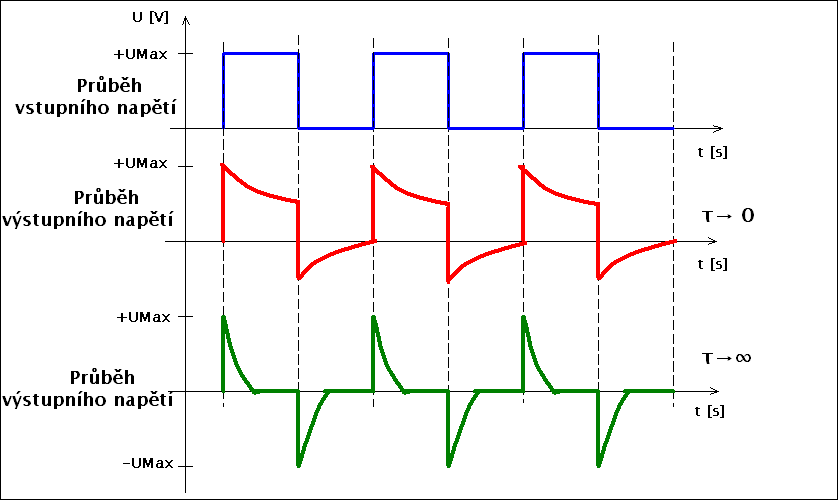 zpět do menu |
|
Multimetr Multimetr je jedním ze základních měřících přístrojů pro měření elektrických obvodů. Obr.č.*****. Na obrázku je vyfocen multimetr měřící základní elektrické veličiny. Střídavý a stejnosměrný proud, napětí a odpor. K tomu ještě umí měřit polovodičové přechody a zesilovací činitel tranzistorů. Multimetry případně ještě mohou měřit další veličiny jako například kapacitu, kmitočet, indukčnost.
Multimetr na obrázku má tak zvaný tři a půlmístný displej. To znamená, že přístroj má tři proměné číslice a na čtvrtém místě vlevo buď nesvítí nic nebo případně se tam zobrazí jednička. Přepínač multimetru na obrázku je nastaven na rozsah 20V, tudíž na tomto rozsahu můžeme měřit napětí do 19,99V. Desetinná tečka udává hodnotu. V našem případě napětí ve voltech. Bude-li například přepínač na rozsahu 200mV, potom desetinná tečka bude veličinu udávat v milivoltech. Rozvítí-li se na displeji pouze jednička, zvamená to, že měřená veličina je větší než nastavený rozsah.
Multimetr má čtyři svorky. Obr.č.****.
Z bezpečnostních důvodů je velikost měřeného napětí omezana na 1000 V stejnosměrných a 750V střídavých. Rozsah pro měření proudů do 20A je doba měření omezena asi na 7s. Tudíž není možné měřidlo používat jako tak zvané panelové, tedy k dlouhodobému měření proudu. Svorka není nijak jištěna a při neodborné manipulaci hrozí nebezpečí úrazu a zničení prístroje.
Multimetr je ovládám jedním přepínačem, jehož polohy jsou rozděleny do několika segmentů. Obr.č.*****. Segment označený:
Změřte dvacet kusů odporů. Odpory seřaďte na papír podle velikosti od nejmenšího do největšího a napiště ke každému odporu naměřenou hodnotu a hodnotu, kterou chtěl výrobce dosáhnout. Tedy hodnotu s řady E12. Dále spočítejte procentuální chybu měřeného odporu. Při měření odporů je nutné dávat pozor, abychom nedrželi vývody odporu oběma rukama. Je to z toho důvodu, že lidské tělo má určitý odpor řádově desítky až stovky kiloohmů. A tento odpor lidského těla by se připojil paraelně k měřenému odporu a zkresloval by naměřenou hodnotu. Čím větší ohmická hodnota měřené součástky, tím větší chyba při měření. Řada E 12: Pasivní elelktronické součástky, tedy odpory a kondenzátory se vyrábí v tak zvaných řadách, což je řada absolutních čísel v jedné dekádě. Nejznámější používanou řadou je řada E12, což znaměná, že v jedné dedádě je dvanáct absolutních hodnot.
1.0; 1.2; 1.5; 1.8; 2.2 ; 2.7; 3.3; 3.9; 4.7; 5.6; 6.8; 8.2 ;
Příklad: Naměříte-li 11,89kΩ, potom v řadě E12 je nejbližší absolutní číselná hodnota 1,2 . Tudíž výrobce chtěl vyrobit odpor 12kΩ a vyrobil ho s přesnotí:
12000 – 11890 = 110Ω , tedy o 110Ω menší.
Odpor byl vyroben s přesností do 1%.
|
|
Měření napětí a proudu
Měření napětí a proudu je jedno ze základních měření v elektronice případně v elektrotechnice. Měření se provádí nejčastěji multimetry, s nímž jsme se seznámili v kapitole, případně ručkovými měřidly. Měříme-li napětí, Vmetr připojíme k měřenému bodu nebo součástce paraelně, při měření proudu Ametr musíme do obvodu, kde chceme změřit proud vložit, tedy musíme obvod rozpojit a Ametr zapojit do serie, tak jak je to znázorněno na obrázku Obr.č. ***
Praktická práce: Spočítej a měřením ověř druhý Kirhofův zákon. Spočítané a naměřené hodnoty zapiš do tabulky.
Schéma zapojení: file:///C:/Users/standastanda/Desktop/www%20p
Zadání: Un = 10V. Vyberte si tři rozdílné libovolné odpory v rozsahu 500Ω až 15kΩ.
Postup: file:///C:/Users/standastanda/Desktop/www/Spočítejte všechny proudy a napětí v obvodu a spočítané hodnoty zapište do tabulky. Následně obvod sestrojte dle schema a všechny proudy a napětí v obvodu změřte a zapište do tabulky. Spočítané a naměřené hodnoty porovnejte.
Příklad výpočtu elektrického obvodu: Un = 10V , R1 = 2Ω, R2 = 5Ω, R3 = 3Ω
Druhý Kirhofův zákon říká: Součet všech úbytků napětí v elektrickém obvodu je roven napájecímu napětí
Un = UR1 + UR2 + UR3 = 2V + 5V + 3V = 10V
Tabulka:
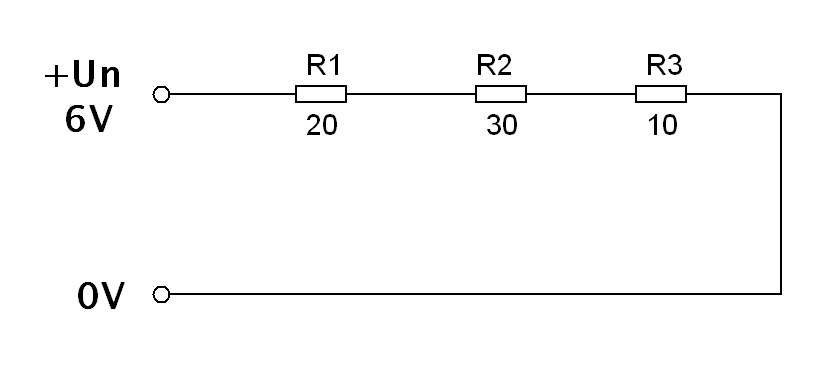
Praktická práce: Spočítej a měřením ověř první Kirhofův zákon. Spočítané a naměřené hodnoty zapiš do tabulky.
Schéma zapojení:
Zadání: Un = 10V. Vyberte si tři rozdílné libovolné odpory v rozsahu 500Ω až 15kΩ.
Postup: Spočítejte všechny proudy a napětí v obvodu a spočítané hodnoty zapište do tabulky. Následně obvod sestrojte dle schema a všechny proudy a napětí v obvodu změřte a zapište do tabulky. Spočítané a naměřené hodnoty porovnejte.
Příklad výpočtu elektrického obvodu:
Un = 10V , R1 = 20Ω, R2 = 50Ω, R3 = 30Ω
První Kirhofův zákon říká: Proud do uzlu přitékající se rovná porudu z uzlu odtékající. V našem obvodu to znamená, že součet proudů v jednotlivých větvích obvodu se musí rovnat proudu tekoucímu ze zdroje.
Ic = IR1 + IR2 + IR3 = 0.5A + 0.2A + 0.33A = 1.03A
Tabulka: file:///C:/Users/standastanda/Desktop/www/
|
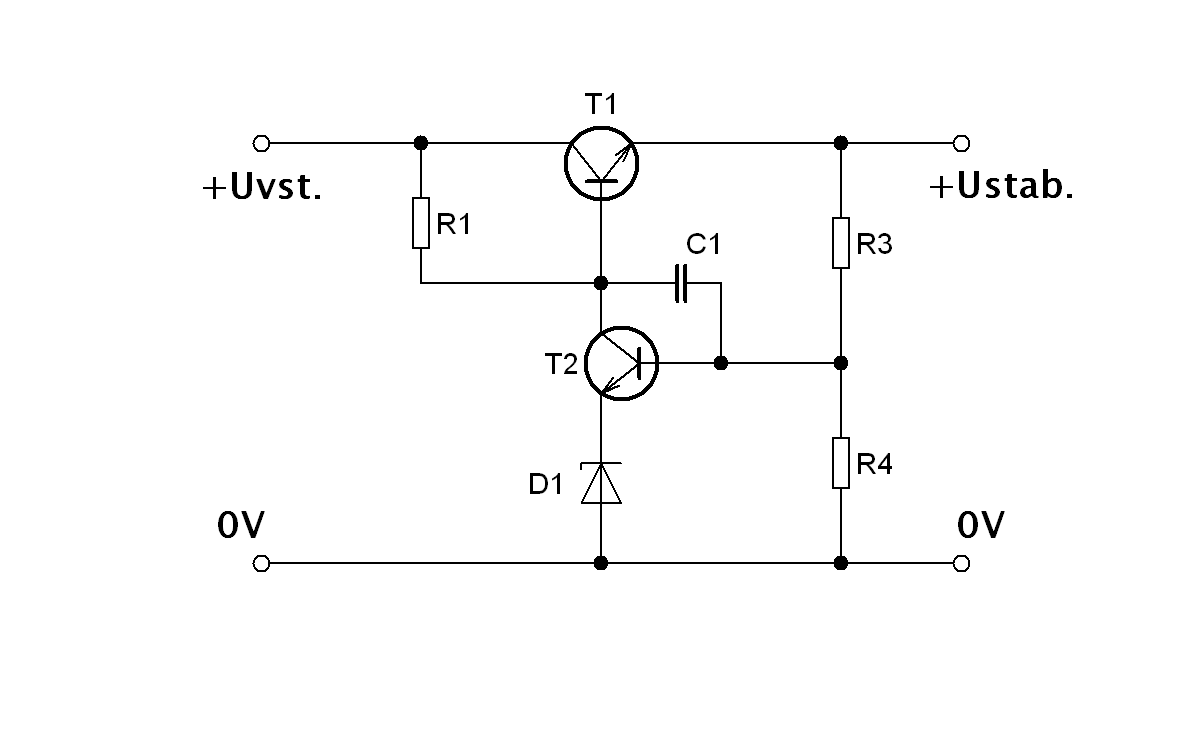
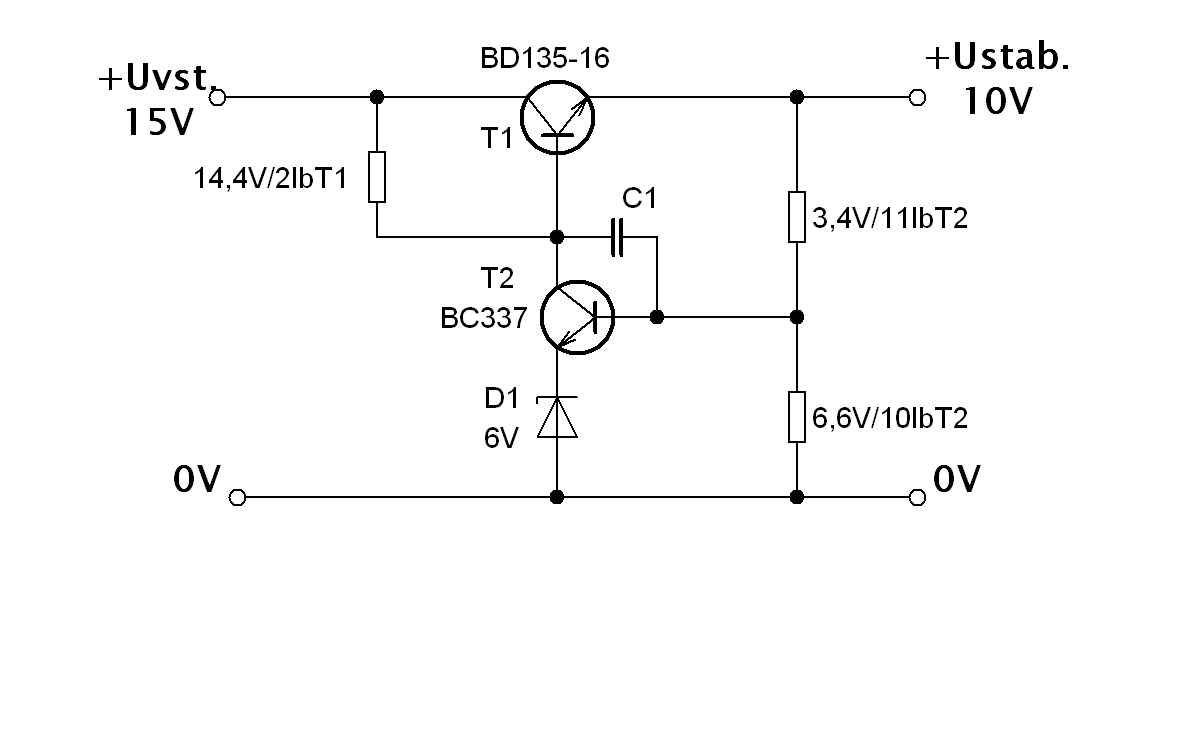
Stabilizovaný zdrojSchéma zapojení: |
||||||||||||||||
|
|
Uvst.= 8V |
+2V |
-2V |
Irzmax = 250mA |
zvlnění |
|
|
C1 |
Ustab. |
|||||
|
Ustab. |
|
|
|
|
|
|
|
Schmittův klopný obvod Schmittův klopný obvod , SKO má dva aktivní prvky , tranzistory T1 a T2 na společném emitorovém odporu. Podobně jako u BKO vždy jsou v inverzních stavech. Po připojení napájecího napětí se tranzistor T2 otevře a T1 zůstane uzavřen přivedeme-li na vstup SKO určité napětí, tranzistory se lavinovitě překlopí do opačného stavu. Pokud napětí klesne pod danou úroveň, tranzistory se překlopí zpět do původního stavu. SKO se mimo jiné hlavně používá jako tvarovač, neboli z jakéhokoliv průběhu napětí vyrobí obdélníkový průběh napětí. Hlavní oblast použití je číslicová technika. Pomocí SKO jsou například ošetřeny všechny vstupy digitálních zařízení.
Schéma zapojení :
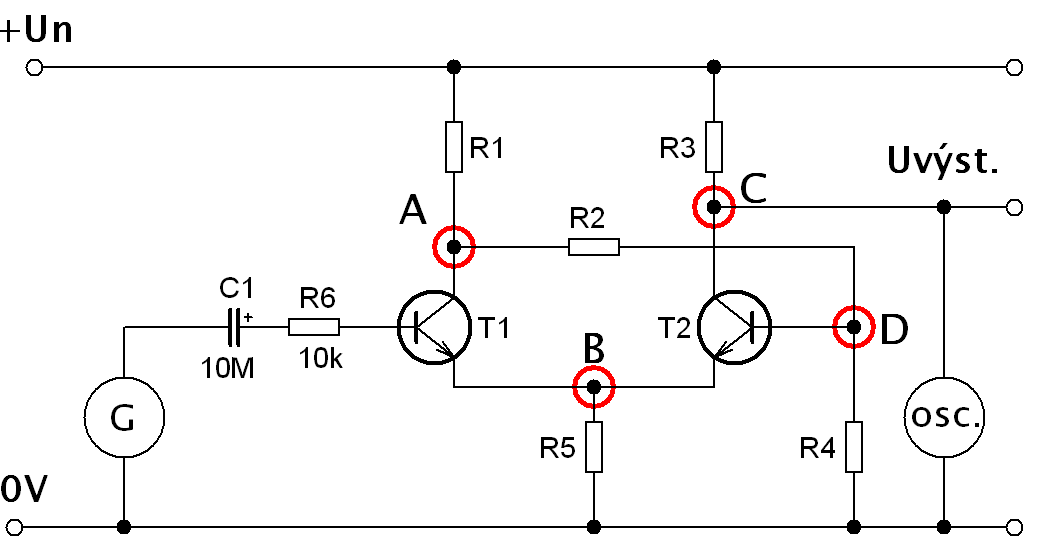
Popis funkce SKO Po připojení napájecího napětí se otevře tranzistor T2 přes odpor R1 děličem v bázi tranzistoru R2 a R4. Napětí v bodě „A“se bude blížit napájecímu napětí. Proud kolektoru trazistoru T2 na společném emitorovém odporu R5 vytvoří určitý úbytek napětí, pro názornost předpokládejme například 1V. Postupně budeme zvyšovat vstupní napětí do báze tranzistoru T1. Ten se ale může otevřít pouze v případě, když mu bude protékat proud bází a to je v okamžiku, je-li báze T1 o 0,6V kladnější než napětí na emitoru tranzistoru T1. V našem případě to nastane, dosáhne-li vstupní napětí úrovně 1,6V. Následně dojde k dvěma procesům vzájemně se podporující. Jednak jak se otevírá T1 tak klesá napětí v bodě“A“, tím se snižuje proud děličem R2 a R4 a tím se snižuje napětí v bodě „D“. A jak se otevírá T1 jeho proud kolektoru postupně zvyšuje úbytek napětí na společném emitorovém odporu R5. Tím T2 dál ztrácí spád napětí mezi bází a emitorem. Celý proces vede k prudkému, říkáme lavinovitému překlopení tranzistorů T1 a T2. Odpor R6 se má ochranou funkci, aby nedošlo k překročení maximálního proudu báze a na funkci SKO nemá vliv. Obvod pracuje s hysterezí, to znamená, že spínací napětí je vyšší, než napětí, při které se obvod překlápí zpět do klidového stavu.
Praktická práce: Spočítejte a měřením odzkoušejte Schmitův klopný obvod jak staticky, to znamená měřením napětí a proudů v obvod, tak i dynamicky pomocí generátoru a osciloskopu.
Schéma zapojení: Obr.č.****
Zadání: IC = 5mA, Un = 10V, UCEsat. = 0,1V Ib spočítejte ze zesilovacího činitele tranzistoru proud děličem Id = 6IB , T1 a T2 jsou univerzální tranzistory malého výkonu, například BC546 Napětí v bodě „B“ UB = 1V
Postup:
do sešitu zakreslete průběh napětí na obrazovce dvoukanálového osciloskopu Uvst./Uvýst.
Příklad výpočtu elektrického obvodu:
IC = 2mA, Un = 12V, UCEsat. = 0,15V, UB = 0,5V, Ib spočítejte ze zesilovacího činitele tranzistoru, proud děličem Id = 6IB T1 a T2 jsou univerzální tranzistory malého výkonu, například BC546
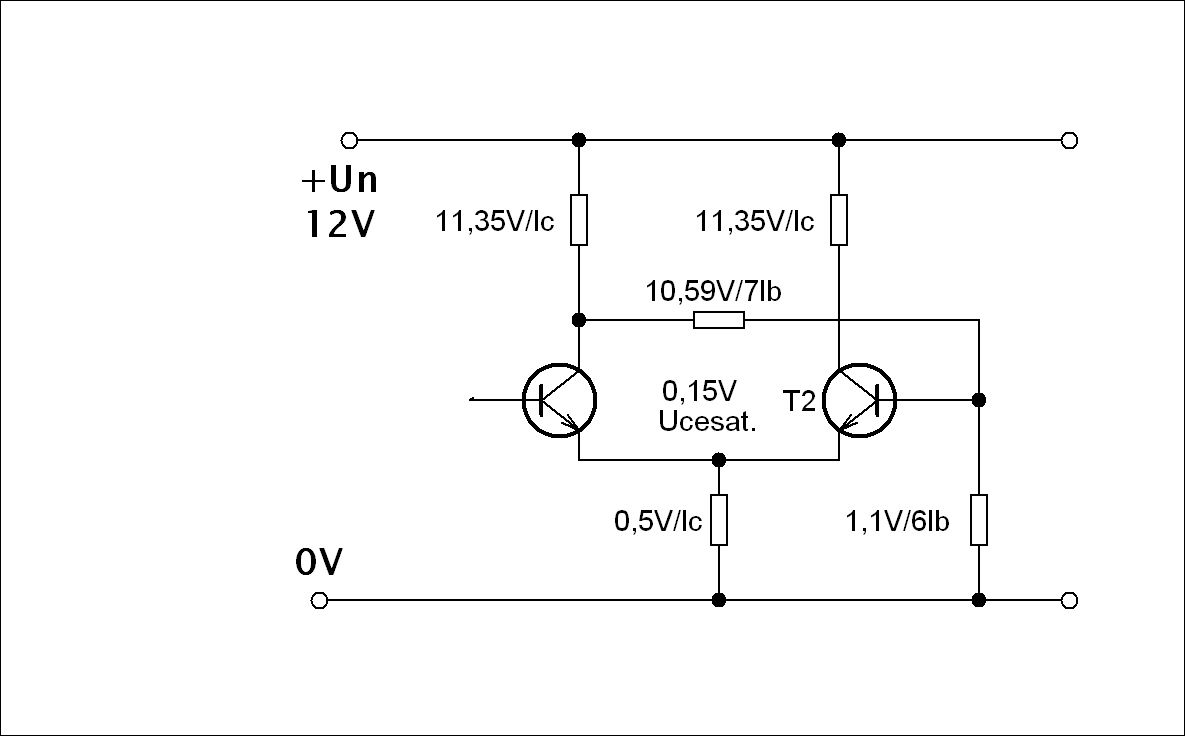
|
|
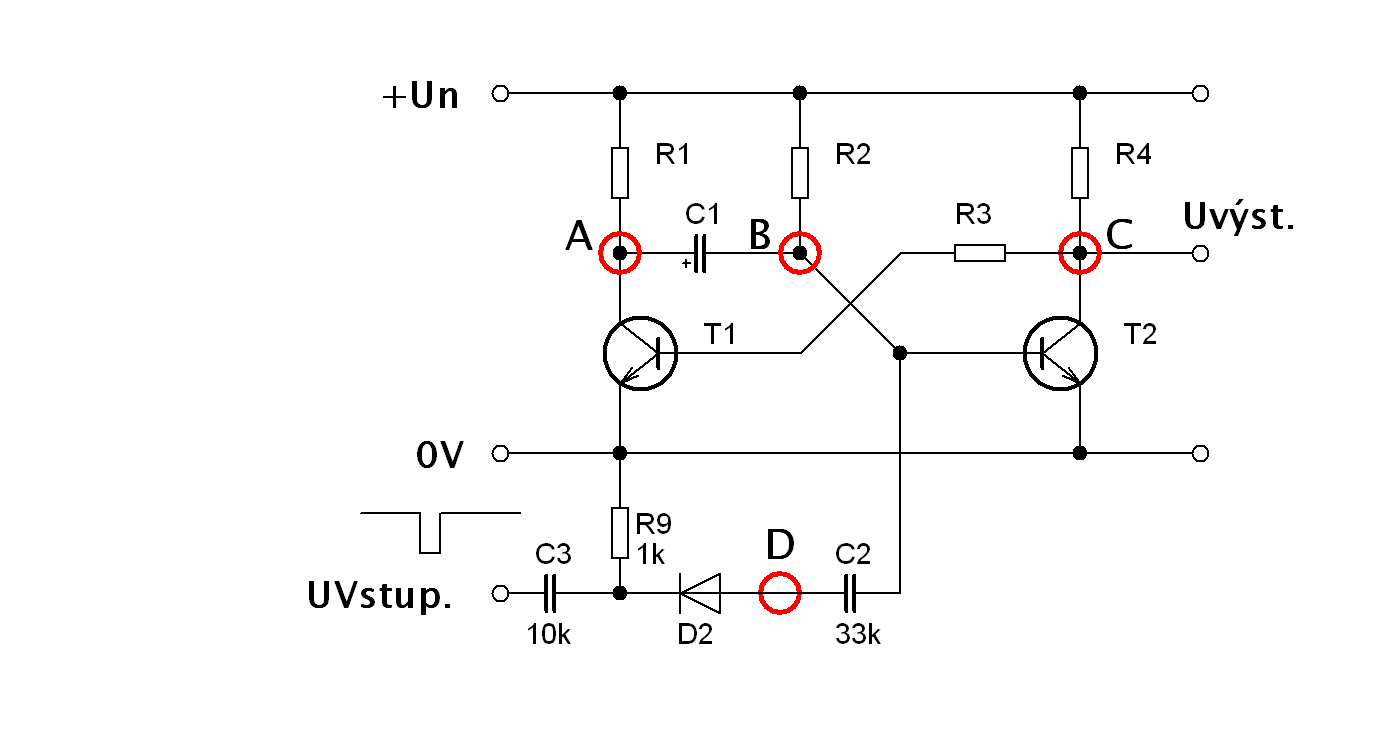
Monostabilní klopný obvod Monostabilní klopný obvod, MKO je elektronický obvod mající jeden stabilní stav. Skládá se ze dvou aktivních prvků, tranzistorů T1 a T2. V základním stavu je tranzistor T1 uzavřen a T2 otevřen. Překlopit tranzistory do opačného stavu je možné dvěma způsoby. Kladným impulsem do báze tranzistoru T1 nebo jak je znázorněno na obrázku záporným impulsem do báze otevřenému tranzistoru T2. Ten se uzavře a na to se tranzistor T1 otevře. Obvod se zpět překlopí po určitém čase, který je dán časovou konstantou Tau, Τ = R2 * C1. Monostabilní klopný obvod vyrobí impuls o určité přesně definované délce t1 = T T = R2 * C1, která je nezávislá na délce vstupního impulsu. V podstatě je to časovač se zpožděným vypnutím. Hlavní oblast použití je oblast číslicové techniky, ale i v analogové elektronice má hojné využití.
Popis funkce MKO Po připojení napájecího napětí se otevře tranzistor T2 přes odpor R2 proudem do báze tranzistoru T2. Napětí v bodě „C“ bude rovno UCESat T2. Nebo-li se bude blížit nulovému napětí. Z toho důvodu se nemůže otevřít tranzistor T1. Jakmile přijde do bodu „B“ záporný impuls, tranzistor T2 se uzavře, napětí v bodě „C“ se bude rovnat napájecímu a na to se otevře tranzistor T1. Napětí v bodě „A“ klesne k nule , tím se v bodě „B“ vygeneruje záporná špička napětí ( viz teorie derivační článek ) a kondenzátor C1 se začne nabíjet přes R2 a otevřený tranzistor T1. Jakmile v bobě „B“ dosáhne hodnota napětí úrovně 0,6V , tranzistor T2 se otevře, napětí v bodě „C“ klesne k nulové hodnotě napětí a T1 se uzavře. Doba překlopení je dána časovou konstantou Tau T = R2 * C1. Funkce obvodu MKO je graficky znázorněna na. Je to průběh napětí v závislosti na čase v různých místech MKO označeny velkými písmeny. Průběh označený například symbolem UD je průběh napětí v bodě „D“ a podobně. Případně je možné výstupní napětí odebírat i z bodu „A“ a tento průběh napětí je inverzní oproti průběhu napětí v bodu „C“
Přibližnou dobu překlopení MKO je možné vypočítat ze vztahu
t1 = 0.7 * R2 * C1 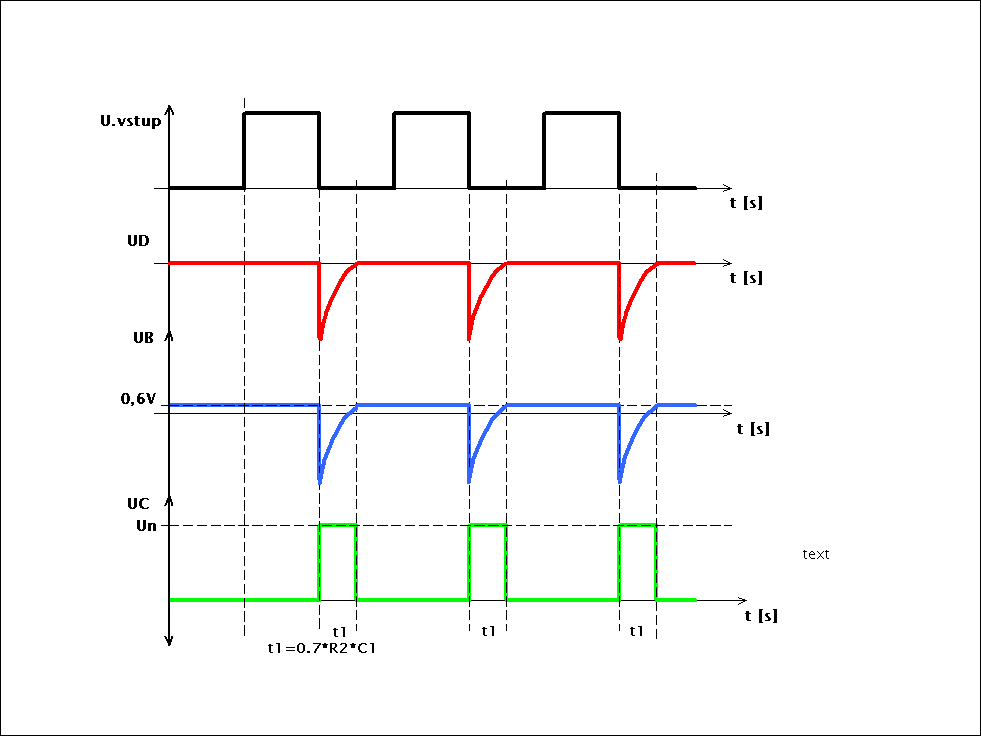
Praktická práce: Spočítejte a měřením odzkoušejte Monostabilní klopný obvod jak staticky, to znamená měřením napětí a proudů, tak i dynamicky pomocí generátoru a osciloskopu.
Zadání: IC = 5mA, Un = 10V, UCEsat. = 0,1V Ib spočítejte ze zesilovacího činitele tranzistoru, z důvodů dobrého nasycení tranzistorů volte 2Ib T1 a T2 jsou univerzální tranzistory malého výkonu, například BC546 Doba překlopení t1 = 1ms
Postup:
Příklad výpočtu elektrického obvodu:
IC = 2mA, Un = 12V, UCEsat. = 0,15V, Ib spočítejte ze zesilovacího činitele tranzistoru, volte 2IB T1 a T2 jsou univerzální tranzistory malého výkonu, například BC546 Doba překlopení t1 = 0.5ms
Obrazovka osciloskopu:
přepínač
časové základny:
Tabulka:
|
|
Operační zesilovače
Operační zesilovač (zkratka OZ) je univerzální stejnosměrně vázaný zesilovací analogový elektronický obvod, jenž je základním prvkem analogových elektronických systémů. Operační zesilovače byly původně vyvinuty pro realizaci matematických operací (odtud pak jejich název) v éře analogových počítačů. První operační zesilovače byly konstruovány z elektronek a později se přešlo na diskrétní polovodičové součástky. Dnešní operační zesilovače jsou téměř výhradně konstruovány jako integrované obvody, přičemž často jeden takový obvod sdružuje několik OZ. První integrované operační zesilovače pocházejí z konce 60. let 20. století. Vůbec první byl obvod μA709, ale ten byl brzy vytlačen obvodem μA741, který je naprostou klasikou ve světě operačních zesilovačů a vyrábí jej mnoho firem v mnoha provedeních dodnes. Oba dva uvedené typy jakož i řada dalších OZ jsou konstruovány pouze z bipolárních tranzistorů. Teprve v 70. letech se začaly v OZ používat unipolární tranzistory. Tyto součástky výrazně zlepšují parametry OZ, takže se téměř blíží ideálnímu OZ. Konstrukce mnohých OZ vybavených unipolárními tranzistory ovšem stále vychází z klasického obvodu 741, u něhož je pouze několik bipolárních tranzistorů zaměněno za unipolární. Operační zesilovač je v podstatě diferenciální, nebo-li rozdílový zesilovač, který má dva vstupy , invertující a neinvertující a jeden výstup. Signál přivedený na invertující vstup je zpracován na výstupu s otočenou fází o 180 stupňů. Signál přivedený na neinvertující vstup je zpracován ve fázi. Přívádíme-li současně napětí na oba vstupy výstupní napětí je potom dané rozdílem vstupních napětí. Invertující vstup je označován znaménkem „ -“, neinvertující vstup je označován znaménkem „+“. Operační zesilovač bývá nejčastěji napájen symetrickým napájecím napětím, a to z toho důvodu, aby výstupní napětí mohlo nabývat kladných a záporných hodnot vůči svorce 0V. Nebo-li abychom nemuseli operačnímu zesilovači nastavovat pracovní bod, tak jak jsme si to ukázali u tranzistorových obvodů, jestliže zpracováváme střídavé napětí mající kladnou a zápornou půl vlnu. Operační zesilovač je často v praxi pro výpočty nahrazován ideálním operačním zesilovačem, jehož základní vlasnosti jsou:
Ideálních vlastností OZ není možné dosáhnout, ale v mnoha případech se k nim blížíme s dostatečnou přesností. Asi největší slabinou OZ ze všech parametrů je šířka kmitočtového pásma, kde kmitočtová charakteristika univezzálního OZ je totožná s dolní kmitočtovou propustí. To znamená, že do určitého kmitočtu tak zvaného mezního je, označován fg, má univerzální OZ stálé zesílení 105, což je bohatě postačující, ale se zvyšujícím se kmitočtem klesá zisk OZ o 6dB na oktávu, až na kmitočtu označovaném ft má zesílení rovno jedné, tehdy už nezesiluje.
Na Obr.č.*** je znázorněno zjednodušené vnitřní zapojení OZ. My už všechny části obvodu známe, už jsme je zapojovali a měřili. Modře orámované tranzistory T1 a T2 je rozdílový zesilovač. Do bází těchto tranzistorů jsou připojeny invertující a neinvertující vstup OZ. Zeleně orámovaný tranzistor T3 je zdroj konstantního proudu. Má za úkol udržovat na emitorech tranzistorů T1 a T2 konstantní teplotně nezávislé napětí. Purpurovou barvou je označen budící stupeň koncového zesilovače a tranzistory T6 a T7 jsou koncové tranzistory zesilovače ve třídě AB.
Na Obr.č.*** je schématická značka operačního zesilovače s popsanými jednotlivými vývody. Některé typy OZ mají ještě kompenzační vstupy napěťové nesymetrie, případně kompenzační vstup kmitočtu. V principielních schématech většinou nejsou uváděny a ani nebývají kresleny vstupy pro napájení. Bere se jako samozřejmost , že OZ je napájen symetrickým napětím. Ale ne vždy to tak musí být. Jsou vyvinuty OZ, které jsou specielně určeny pro nesymetrické napájení. Není to typické a potom samozřejmě musí být napájení příšlušně označeno.
Základní funkce OZ
Invertující operační zesilovač Invertující zesilovač je jedno z nejpoužívanějších zapojení. Na výstupu se objeví vstupní napětí vynásobené napěťovým zesílením Au nebo-li ziskem OZ., ale s obrácenou fází o 1800 (tedy zinvertované). Velikost zesílení je daná poměrem odporů R2 a R1, Obr.č.*** Au = Ovšem pozor - tento vzorec platí jen tehdy, je-li zdrojem signálu obvod s nulovým vnitřním odporem (tedy obvod, chovající se jako ideální zdroj napětí). Pro výstupní napětí platí vztah Uvýst = - Uvst *
Vstupní impedance je schodná s ohmickou hodnotou odporu R1. Zvst = R1. Protože Oz se snaží mezi vstupy udržet nulové napětí (viz teorije rozdílový zesilovač) potom na invertujícím vstupu je t.zv. plovoucí zem nebo říkáme že v tomto místě je virtuální nula. Při výpočtu odporů R1 a R2 si odpor R1 zvolíme a druhý dopočteme dle zadání. Odpor R1 nejčastěji volíme desítky kiloohmů.
Praktická práce: Spočítejte a měřením ověřte invertující operační zesilovač
Zadání: Un = ±15V, napěťový zisk AU = 2 vstupní napětí v rozsaho -2V ÷ +2V R1 = 10kΩ
Popis funkce: Vlastní OZ je popsán v předešlé kapitole. Tento obvod je doplněn odporem R3, který pracuje jako kompenzace proudové nesymetrie OZ. Na vlastní činnosti OZ se nijak nepodílí. Pro malá zesílení se volí R3 = R1. V zapojení je použit snad nejpoužívanější a nejznámější OZ μA741. Je zde použita kompenzace napěťové nesymetrie dle katalogu výrobce na vývodech OZ 1 a 5 trimrem 10k.
Postup:
Tabulka:
|
|
Neinvertující
operační zesilovač
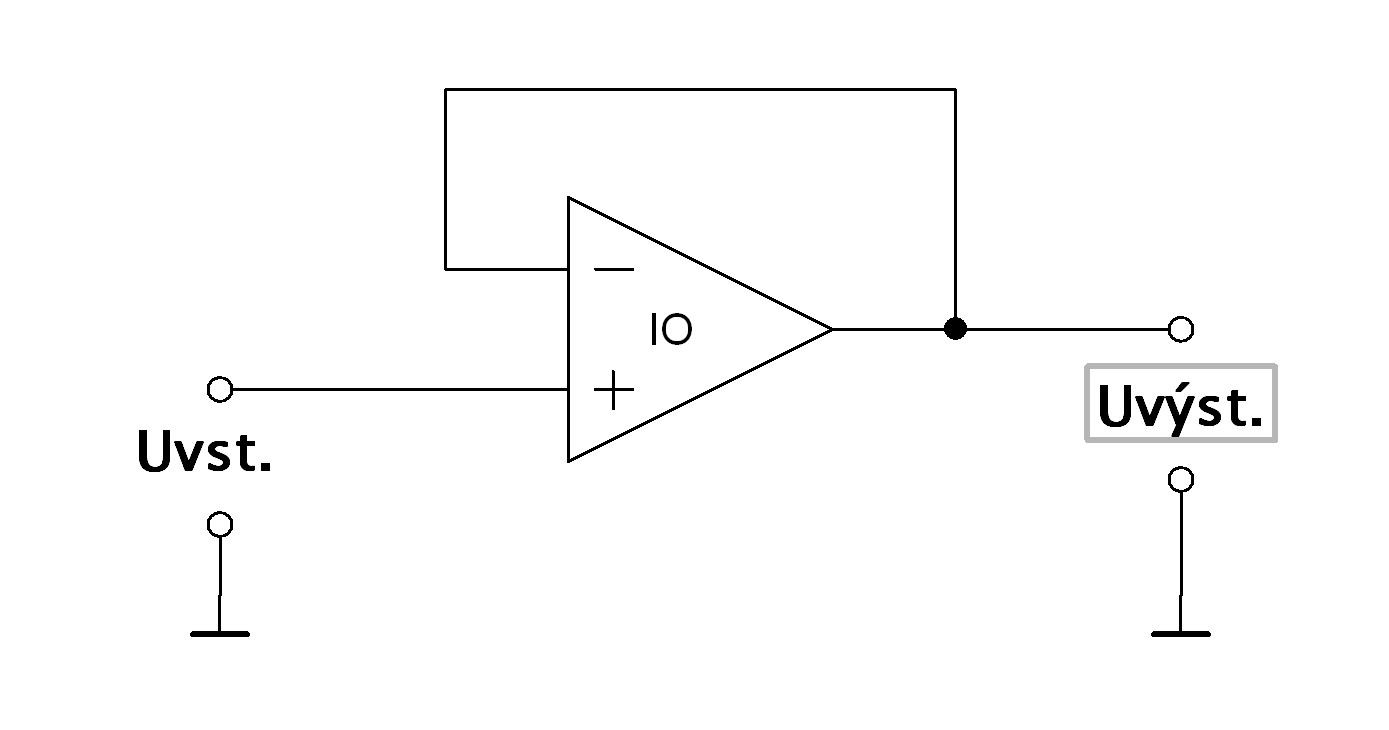
Výstupní napětí neinvertujícího zesilovače je ve fázi se vstupním napětím. Zisk neinvertujícího zesilovače je dán vztahem.
Au = 1+ R2/R1
Pro výstupní napětí potom platí. Uvýst = Uvst * R2/R1
Z matematických vztahů je zřejmé, že neinvertující zesilovač má zisk vždy větší než jedna. Hlavní výhodou tohoto zapojení je velký vstupní odpor, který je nezávislý na ohmických hodnotách odporů R1 a R2. Reálná hodnota vstupního odporu je 1MΩ ÷ 10TΩ. Hodnotu odporu R1 volíme nejčastěji v jednotkách, případně desítkách kiloohmů. Zvláštním případem neinvertujícího zesilovače je sledovač napětí. Napěťový zisk je roven jedné a napětí vstupní a výstupní je ve fázi. Má velmi velkou vstupní impedanci, 1MΩ ÷ 10TΩ, a malou výstupní impedanci. Sledovač se používá pro oddělení vysokoimpedančního vstupu a nízkoimpedančního výstupu. Uvýst. = Uvst. Zvst. = nekonečnu
Praktická práce: Spočítejte a měřením ověřte neinvertující operační zesilovač
Zadání: Un = ±15V, napěťový zisk AU = 2 vstupní napětí v rozsahu -2V ÷ +2V R1 = 10kΩ
Popis funkce: V zapojení použijte OZ μA741 s kompenzací napěťové nesymetrie dle katalogu výrobce na vývodech OZ 1 a 5 trimrem 10k.
Postup:
Au = 1+ R2/R1
Uvýst = Uvst * R2/R1
Tabulka:
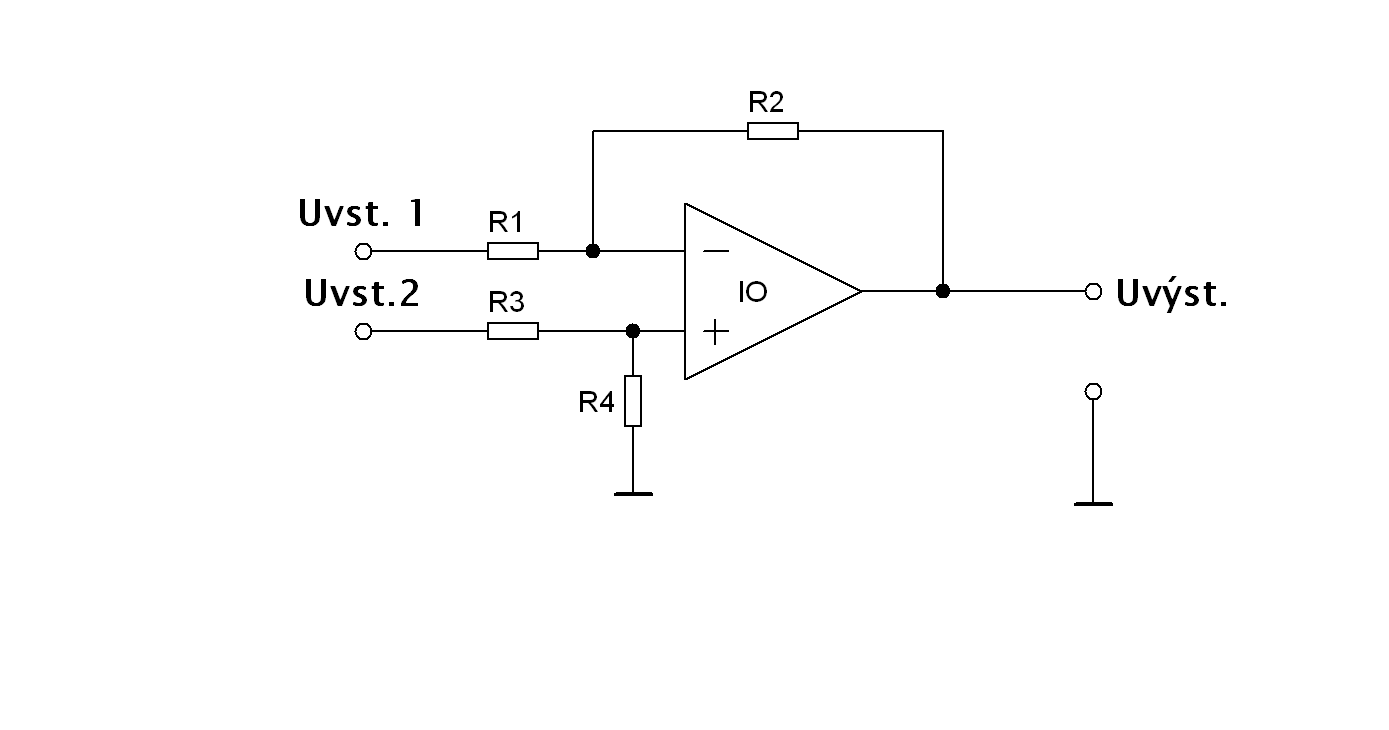
Rozdílový zesilovač Rozdílový zesilovač můžeme v literatuře nalézt taky pod názvem diferenciální zesilovač. Zpracovává napětí současně z obou vstupů. Jsou-li vstupní napětí nesouhlasná polaritou hodnoty napětí sečte a vynásobí ziskem OZ. Jsou-li polaritou souhlasná, napětí od sebe odečte a výsledek vynásobí ziskem OZ.
Au = R2 / R1
Vztah pro výpočet výstupní napětí. Uvýst. = (Uvst.2 - Uvst1) * R2 / R1
K vytvoření pracovních podmínek obou vstupů je třeba aby R1 = R3, R2 = R4. Pak se jako užitečný signál uplatní pouze rozdíl vstupních napětí a rušivé signály jsou potlačeny. Diferenciální zesilovač obvykle vyžaduje kompenzaci napěťové nesymetrie.
Praktická práce: Spočítejte a měřením ověřte rozdílový zesilovač Schéma zapojení:
Zadání: Un = ±15V, napěťový zisk AU = 1 vstupní napětí v rozsahu -2V ÷ +2V R1 = 10kΩ
Popis funkce: V zapojení použijte OZ μA741 s kompenzací napěťové nesymetrie dle katalogu výrobce na vývodech OZ 1 a 5 trimrem 10k.
Postup:
Au = R2 /R1
Uvýst. = ( Uvst.2 - Uvst1) * R2 / R1
Příklad výpočtu elektrického obvodu:
Un = ±15V, napěťový zisk AU = 2 vstupní napětí v rozsahu -2V ÷ +2V R1 = 10kΩ Uvst.1 = -1V a Uvst.2 = +1V
Au = R2 / R1 , R2 = Au * R1 = 2 * 10kΩ = 20kΩ
R4 = R2 , R3 = R1
Uvýst. = = [ +1V - (-1V)] = +2V * 2 = 4V
Tabulka:
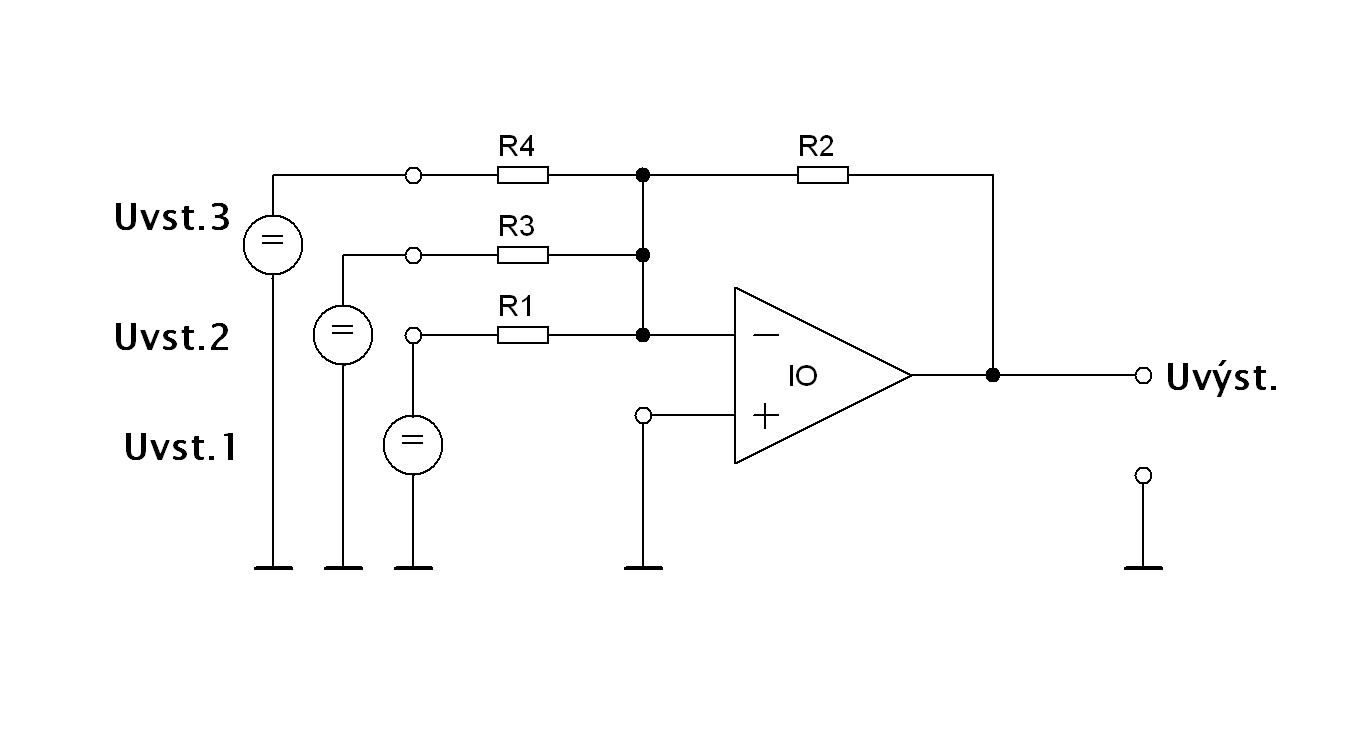
Sčítací zesilovač Sčítací operační zesilovač nebo jiným názvem sumátor sčítá napětí na jednotlivých vstupech, přičemž výstupní napětí je fázově otočeno o 180 stupňů.
Sčítací zesilovač má obdobné vlastnosti jako invertující zesilovač. Zesílení pro jednotlivé vstupy je dáno poměrem odporu R2 a vstupních odporů. Vstupní impedance určitého vstupu je rovna hodnotě vstupního odporu. Pokud je polarita jednotlivých vstupních napětí stejná, potom se jednotlivá vstupní napětí vynásobí ziskem pro daný vstup a na výstupu OZ se vstupní napětí sečtou s opačnou fází.
Zesílení Uvst.1 je Au1 = R2 / R1 Zesílení Uvst.2 je Au2 = R2 / R3 Zesílení Uvst.3 je Au3 = R2 / R4 Potom platí : Uvýst. = – (R2 / R1 * U1 + R2 / R3 * U2 + R2 / R4 * U3) Nečastěji se používá sčítací zesilovač pro Au = 1 na všech vstupech stejné. Potom platí. R2
= R1 = R3 = R4
Praktická práce: Spočítejte a měřením ověřte sčítací operační zesilovač
|